Week 7 Reflection

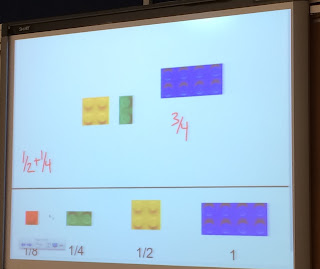
This week we looked at Chapter 22 of the textbook, Patterns and Algebra. I was a bit worried before I started doing the readings, because algebra can be rather intimidating. I don't remember if I was particularly 'good' at algebra when I was in school, so I was a bit worried about this topic. We didn't go too into depth about algebra in our peer taught lessons, we focused more on patterns. There are lots of good tips and strategies for teaching algebra in our textbook (Marian Small provides some of the best strategies), so I am not too worried about teaching it if I have to.

Since this weekend is Halloween, the teacher candidates who taught this week decided to associate the holiday with math, to make it fun. I know I definitely enjoyed these Halloween-themed lessons, so I'm sure it would have been a big hit with kids. I will most definitely try to incorporate holiday themed lessons into my own teaching, to try to engage kids and make things more interesting. I think this is a great strategy to use to get kids excited about math. Halloween-themed math was really tasty, and if I enjoyed it, I'm sure kids would have gone ballistic over having candy to use as a manipulative. We learned about patterning and the rules that go along with it, and we got to create our own patterns using candy. I thought this was a really great idea, and I enjoyed the snack! One of the things we looked over was the core of the pattern; you should include at least 3 repetitions so that students can fully identify the core. Below is the pattern I created using M&M's and Hershey's kisses, with my 3 repetitions of the core pattern:

Woolley, E. © 2015 

I thought this was a fun and creative idea to use candy as a manipulative. Another worksheet that I thought was awesome (and Halloween-themed) was about finishing the pattern, and identifying the pattern sequence. It used pictures to to show patterns, but also found a way to use number patterns (at the bottom of the worksheet), but still managed to make it fun (numbers inside pictures of pumpkins). I think it was really well put together, and a fun way to get kids to practise using patterns. I'm going to save this resource to use in my own classroom.

Woolley, E. © 2015 

 One of the algebra resources that I thought was really cool was trying to identify the word problem with the algebraic expression. I think this was a really smart resource because it helps show students that you can apply real-world situations to algebra. It helps show that algebraic expressions are not just numbers and letters that don't make sense, but you can visualize the problem and find the missing variable to find the answer. The students match up the green pieces of paper, one with the word problem and the other with the algebraic expression. Once they match these up, they can use the blue handout to find what the missing variable is, and complete the equation.

Woolley, E. © 2015 

If students get really confused, they can download the free app on their mobile device called photo math, to take a picture of the equation, and it will solve the problem for them, showing the steps on how the problem was solved. I think this is a valuable resource because it shows students the steps they need to follow to solve the problem, and how to solve similar problems. However, if students use this app to solve all their problems without trying to solve it themselves, they won't learn. If I show this app to my students and allow them to use it, I will only let them use it for really tricky problems that they need extra help with. 

Week 6 Reflection

This week you have we read chapter 13 in the textbook which focused on ratio, rate, and percent, but in class we mainly talked about proportional reasoning. We only had one peer present this information to us this week, but it was still quite interesting to learn about. We talked about part-to-part ratios and part-whole ratios in class. This can be a bit of a confusing topic for some students, but with good examples it is can become clearer. We also looked at equivalent rations, which is when two ratios represent the same relationship. For example 3:4 = 6:8. It is much like equivalent fractions, you just have to multiply both numbers by the same number. We went over ratios and rates, and we looked at some good strategies that will help students visualize rate and ratio problems. The handout that we got had this information: 

Woolley, E. © 2015 

Woolley, E. © 2015

Some of the manipulatives that can be used to solve these problems include:

• counters/grids 
• ratio tables/charts - double number lines 
• graphs 
• multiplication tables - easy to visual equivalent ratios - double it, triple it, etc. and you have your equivalent ratios 

We looked at  a video that showed students problem solving the Chocolate question 

• absolute cost is the same
• goal - get the student differentiate absolute cost and relative proportional cost 
• i.e. cost per unit 
• 1 chocolate bar 1200g for $10 
• 1 chocolate bar 1.3kg for $10 
• first convert to same unit - 1200g and 1300g 
• both $10 (absolute cost is the same) but one chocolate you get 100g more chocolate for the same price 

The students problem solved the problem and shared their thoughts with the class. 

It went over what informal proportional reasoning is; one student explained the answer, some students didn't understand so she rephrased her answer to make sure everyone understood the problem and the answer and the reason for her thinking. She provided evidence for her thinking and explained her logic. This video was a good example of how to teaching math to younger students and how to get them engaged.  

For the last part of class we talked about the 3-part lesson plan, which is used in most math lessons. We filled in lesson plan template with the model from the video. This way we will be able to understand how to follow the template when we have to write our own lesson plans. Within the 3-part lesson plan there are 7 steps that we have to go through to plan for a math lesson:

1. Do the math
2. Questions to ask
3. Problems to pose
4. Instructional strategies 
5. Resources/materials
6. Assessment 
7. Adaptations/modifications/extensions 

We also went over a few examples of success criteria for Sharing Your Work in a math class:

• I can represent my work with a diagram or picture or chart
• I can select a strategy and use operations to show my work
• I can explain the actual steps I took to solve my problem 

Overall, this class was very helpful and informative for writing our own lesson plans in math. I will definitely be using this information to help me teach math and plan a lesson plan.

Week 5 Reflection

This week in class we had more student presentations. We talked about integers, more specifically the order of operations of integers, multiplying and dividing integers, and perfect squares. 

multiplication and division of integers. 

First we looked at the multiplication of integers. As usual, I was fairly lost in the subject, since I don't remember most of the math that I learned in elementary school. Thankfully, the textbook and my peers explain things very well, so I was able to comprehend what was happening. My peers always give great examples of multiple manipulatives that we can use with our students to help make problems clearer. This week we were shown how to use number line charts, integer tiles, and counters to help solve problems involving integers. We also went over what product and quotient means. 

• product - the answer when 2 or more numbers are multiplied together 
• quotient - the result obtained by dividing one quantity by another

Then, we went over the order of operations, which doesn't solely apply to working with integers. This is one of the things I actually remember learning in school; BEDMAS or PEDMAS, which stands for brackets/parenthesis, exponents, divide, multiply, add, subtract. We use this when a math problem has more than one operation in it. We talked about how you can divide or multiply first, since it does not affect the solution, but other than that you must follow the correct order of BEDMAS for all other operations. We also went over the revision of powers, for example, 2^(2^2) = 16. This was helpful for me, so I can explain to my students how to figure these types of problems out. 

One of the things I enjoy in this class is finding ways to use math in everyday life. I like finding examples of using math in everyday uses, to prove to students that knowing math is actually useful (contrary to what they believe). Last week we talked about decimals and a real world example was adding money/change. This week we were talking about integers, so the real world example was temperature. 

Woolley, E. © 2015

One of the other things we looked at this week was number sense and numeration: perfect squares and square roots. As a refresher, perfect squares are any number that is the product (multiplication) of 2 equal integers. Square roots are the reverse side of perfect squares; they are a value that can be multiplied by itself to give the original number. We looked at a fun math problem related to perfect squares and square roots. It's called the Locker Problem, and it is explained here. We expect students to be able to use the square root button on their calculators in order to solve these problems, but this problem actually makes them think. I found this porblem challenging, but fun at the same time. It was really educational and I hope to challenge my students with it. Finally, a fun fact that one of our peer teachers shared with us is square root day: 04/04/16, or April 4, 2016.

We looked at two fun math parody videos, that proved how some people enjoy math, and can have fun with it. They made our whole class laugh, a room full of adults and teacher candidates, so I'm sure a room full of elementary students would love watching this, and hopefully be inspired to make their own, fun math video. 

Science and Math War

What is the value of Pi?

Week 4 Reflection

This week we discussed many things in class and in the readings. We looked at decimals and fractions, and how to add, subtract, multiply, and divide decimals and fractions. It was a great review for me, since I have not done this type of math in many years, only having to add decimals occasionally when paying bills. Having to actually figure out how to use the different operations to solve the problems without a calculator was a bit challenging for me in the beginning, but after viewing some of the great tips that my peers taught, I am more confident in my own abilities to solve these kinds of problems, which means I will be able to effectively teach my own students these great ways to solve math problems involving fractions and decimals.

We looked at some really great ways to subtract decimals. We were shown many different visual aids to solve these problems, which I will definitely be using in my own instruction. I think they're great for students, especially for visual learners. We coloured in 10x10 grids and then took away the amount we were subtracting. This was the same concept, but we used physical blocks as the manipulative (which is a great method for tactile learners). I think it is really good to know these methods, especially for students who struggle with subtracting decimals. Another great method for adding and subtracting decimals is the use of money, since we all use money, and kids are generally fascinated by the concept of money, I think I will use this method when teaching about decimals. Since quarters, dimes, and pennies are in the decimals, it is a good visual for students. This will also help them with a real life situation that students crave (students generally don't want to learn math because they say they will "never use it in everyday life"). We also looked at how to multiply and divide decimals. I forgot about some of these helpful methods, so it was a good refresher to have. Multiplying and dividing decimal numbers is the same as multiply and dividing whole numbers, you just have to ignore the decimal until you have solved the problem, and then add it in its appropriate place. One method that I particularly enjoyed was using the 10x10 grid and colouring in the first amount and then dividing it. 

Woolley, E. © 2015

It was a great visual aid, and I personally understood what it meant to divide decimal numbers. It kind of blew my mind, which is why I really like this method. Understanding that dividing is just grouping the first number into groups of the second number really helped, and this method actually showed me this. Hopefully my students will understand much better, like I did, by using this method.

Another cool method was using the smartboard as a visual. Instead of using physical objects, one person showed us how to use images that represent fractions. This was something that shocked everyone in the class, and I think we will all want to learn how to use smartboards to show our students how to add/subtract fractions using visuals.  

Woolley, E. © 2015

Finally, I am starting to appreciate math more, especially learning all these great new methods. I'm actually having fun with math, which is something I never thought I would say. Hopefully this will make me a much better math teacher, and I will be able to inspire my students to have fun with math as well. One of the optional links that I was playing around with led me to this game where you practise adding fractions by making smoothies. I actually played with it for a good 30 minutes before I realized that I was playing a math game and actually enjoying it! I'm glad that I am learning that math can be fun and that I am discovering good and interactive methods that I will be able to help my students learn better.